Qudit Cirq Library

Tutorial

This tutorial provides a guide on how to use the Qudit Cirq Library, including creating qudits, applying qudit gates, building circuits, and simulating quantum computations with qudits.

Qudits are \(d\)-level quantum systems which serve as the generalization of qubit systems (\(d = 2\)). Theoretically, we assume that they lie in the \(d\)-dimensional complex Hilbert space \(\mathbb{C}^d\). Assume that we have the computational basis \[ \{ \ket{s} : s \in \mathbb{Z}_d \} \] of \(\mathbb{C}^d\), where \(\ket{s}\) is a column vector of \(d\) dimensions with zeros everywhere except at position \(s\), where it is \(1\).

The general form of a qudit \(\ket{\psi}\) is:

\[ \ket{\psi} = \sum_{j = 0}^{d-1} \alpha_j \ket{j}, \]

with the condition that \[ \sum_{j = 0}^{d - 1} |\alpha_j|^2 = 1, \] and \(\alpha_j \in \mathbb{C}\). For an introduction to qudit systems, see for example Asghar, Mukherjee and Brennen [2024] (https://doi.org/10.48550/arXiv.2409.04026), and the references therein.

Table of Contents

Creating Qudits

Qudits are created using Cirq's LineQid class with a specified dimension. Here's how you can create a qudit of dimension d:

import cirq

# Create a qudit of dimension d = 10
qudit = cirq.LineQid(0, dimension=10)

To create any other initial state \(\ket{s}\) for \(s \in \mathbb{Z}_d\), you can use the following code:

import cirq
import numpy as np 

d = 10
s = 3
initial_state = np.zeros(d, dtype=complex)
initial_state[s] = 1

Qudit Gates

The Qudit Cirq Library provides implementations of common quantum gates.

Qudit Pauli-X Gate (quditXGate)

The qudit Pauli-\(X\) gate generalizes the bit-flip operation to \(d\) dimensions. Its operation on the computational basis state \(\ket{s}\) is defined as:

\[ X\ket{s} = \ket{s + 1} \]

from qudit_cirq.qudit import quditXGate

# Create a qudit X gate for dimension d=3
x_gate = quditXGate(d=3)

Qudit Pauli-Z Gate (quditZGate)

The qudit Pauli-\(Z\) gate generalizes the phase-flip operation. Its operation on the computational basis state \(\ket{s}\) is defined as:

\[ Z \ket{s} = \omega^s \ket{s} \]

from qudit_cirq.qudit import quditZGate

# Create a qudit Z gate for dimension d=3
z_gate = quditZGate(d=3)

Qudit Hadamard Gate (quditHGate)

The qudit Hadamard gate sends computational basis states into equal superpositions in \(d\) dimensions. Its operation on the computational basis state \(\ket{s}\) is defined as:

\[ H\ket{s} = \frac{1}{\sqrt{d}}\sum_{j = 0}^{d-1} \omega^{js} \ket{j} \]

See for example Wang et al. [2020] ( https://doi.org/10.3389/fphy.2020.589504).

from qudit_cirq.qudit import quditHGate

# Create a qudit Hadamard gate for dimension d=5
h_gate = quditHGate(d=5)

Qudit Controlled-NOT Gate (quditCNOTGate)

The qudit Controlled-NOT gate generalizes the CNOT operation. This is a two-qudit operation with two inputs: a control qudit and a target qudit. Given two computational basis states, its action is defined as:

\[ \ket{r}\ket{s} \rightarrow \ket{r}\ket{r + s} = \ket{r} X^r \ket{s} \]

from qudit_cirq.qudit import quditCNOTGate

# Create a qudit CNOT gate for dimension d=4
cnot_gate = quditCNOTGate(d=4)

Qudit \(S\) Gate (quditPhaseGate)

The qudit \(S\) gate generalizes the phase gate to dimension \(d\). Its operation on the computational basis state \(\ket{s}\) is defined as:

\[ S\ket{s} = \omega^{s(s+p_d)/2} \ket{s}, \]

where \(p_d = 1\) if \(d\) is odd, and \(0\) otherwise. This is one of the generators of the qudit Clifford group, along with the Pauli-\(Z\) gate, the qudit Hadamard gate, and the controlled-\(Z\) gate. See for example Jafarzadeh et al. [2019] (https://doi.org/10.48550/arXiv.1911.08162).

from qudit_cirq.qudit import quditPhaseGate

# Create a qudit Phase gate for dimension d=5 (prime and odd)
phase_gate = quditPhaseGate(d=5)

Qudit Controlled-\(Z\) Gate (quditCZGate)

The qudit Controlled-\(Z\) gate generalizes the same operation on qubits. This is a two-qudit operation with two inputs: a control qudit and a target qudit. Given two computational basis states, its action is defined as:

\[ \ket{r}\ket{s} \rightarrow \omega^{rs}\ket{r}\ket{s} = \ket{r}Z^r \ket{s} \]

This is one of the generators of the qudit Clifford group, along with the Pauli-\(Z\) gate, the qudit Hadamard gate, and the controlled-\(Z\) gate. See for example Jafarzadeh et al. [2019] (https://doi.org/10.48550/arXiv.1911.08162).

from qudit_cirq.qudit import quditCZGate

# Create a qudit CZ gate for dimension d=5 (prime and odd)
cz_gate = quditCZGate(d=5)

Qudit \(U_{\pi/8}\) Gate (quditU8Gate)

The \(U_{\pi/8}\) gate generalizes the qubit \(\pi/8\) gate to qudits (called the \(T\) gate in the classic text from Chuang and Nielsen [2010]). The extension to qudits is defined for a prime dimension \(d\). The general form of the gate is defined as:

\[ U = \sum_{j = 0}^{d-1} \omega^{v_j} \ket{j}\bra{j} \]

The exact values of the \(v_j\)'s depend on the dimension \(d\). Explicit formulas to compute these values for \(d = 3\) and \(d \geq 5\) (remember \(d\) should be a prime) are given in Howard and Vala [2012] (https://doi.org/10.48550/arXiv.1206.1598). Our implementation of this gate follows their construction.

from qudit_cirq.qudit import quditU8Gate

# Create a qudit U_{pi/8} gate for dimension d=7
u8_gate = quditU8Gate(d=7)

Building Circuits with Qudits

There are two primary methods for building circuits with qudits:

Method 1: Manual Construction

Manually create circuits by explicitly defining qudits and appending gates.

import cirq
from qudit_cirq.qudit import quditXGate, quditHGate, quditCNOTGate

# Create qudits
qudit1 = cirq.LineQid(0, dimension=3)
qudit2 = cirq.LineQid(1, dimension=3)

# Build a circuit
circuit = cirq.Circuit()
circuit.append(quditHGate(d=3).on(qudit1))
circuit.append(quditCNOTGate(d=3).on(qudit1, qudit2))

Gates are appended to the circuit using the .append() method.

Method 2: Using create_circuit Function

Use the create_circuit function for a more concise syntax when building circuits.

from qudit_cirq.qudit import quditHGate, quditCNOTGate, qudit_measure

# Build the circuit using create_circuit
circuit, qudits, qudit_order = create_circuit(
    3,  # Set dimension d=3
    (quditHGate, 'q0'),
    (quditCNOTGate, ['q0', 'q1']),
    (qudit_measure, 'q0'),
    (qudit_measure, 'q1')
)

Arguments:

1. The function accepts a variable number of arguments (*args).
2. Dimension is set by passing an integer.
3. Gates are specified as tuples with the gate type and qudit names.

Returns:

1. circuit: The constructed cirq.Circuit.
2. qudits: A dictionary mapping qudit names to cirq.Qid objects.
3. qudit_order: A list of qudits in the order they were added.

Extended Usage of create_circuit Function

Dimensions for each qudit can be specified explicitly:

circuit, qudits, qudit_order = create_circuit(
    (3, quditHGate, 'q0'),
    (4, quditHGate, 'q1'),
    (5, quditTGate, 'q3'),
    (6, quditTGate, 'q4')
)

Measurement and Simulation

You can measure the qudits and simulate the circuit.

Measuring Qudits

For manual circuits:

circuit.append(cirq.measure(qudit1, key='q1'))
circuit.append(cirq.measure(qudit2, key='q2'))

For circuits built with create_circuit, measurements are included during construction.

Simulating the Circuit

Use Cirq's simulator to run the circuit and obtain measurement results.

# Simulate the circuit
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=10)

# Print the results
print(result)

Examples

Example 1: Qudit GHZ State Preparation (Manual Construction)

Prepare a GHZ state using qudits of dimension 3.

import cirq
from qudit_cirq.qudit import quditHGate, quditCNOTGate

# Parameters
d = 3  # Qudit dimension
n_qudits = 3  # Number of qudits

# Create qudits
qudits = [cirq.LineQid(i, dimension=d) for i in range(n_qudits)]

# Build the circuit
circuit = cirq.Circuit()
circuit.append(quditHGate(d).on(qudits[0]))
for i in range(1, n_qudits):
    circuit.append(quditCNOTGate(d).on(qudits[i - 1], qudits[i]))

# Measure
circuit.append(cirq.measure(*qudits, key='result'))

# Simulate
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=10)
print(result)

Example 2: Qudit GHZ State Preparation (Using create_circuit Function)

Prepare the same GHZ state using the create_circuit function.

from qudit_cirq.qudit import quditHGate, quditCNOTGate, qudit_measure

# Build the circuit using create_circuit
circuit, qudits, qudit_order = create_circuit(
    3,  # Set dimension d=3
    (quditHGate, 'q0'),
    (quditCNOTGate, ['q0', 'q1']),
    (quditCNOTGate, ['q1', 'q2']),
    (qudit_measure, 'q0'),
    (qudit_measure, 'q1'),
    (qudit_measure, 'q2')
)

# Simulate
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=10)
print(result)

Utility Functions

The Qudit Cirq Library provides multiple utility functions to assist with formatting outputs, printing state vectors, and performing tensor products.

Formatting Output (format_out)

The format_out function formats a NumPy matrix or vector for display, allowing you to specify the output type for better readability.

Function definition:

def format_out(matrix, output_type='float'):
    # Function implementation

Parameters

1. matrix: The NumPy array (matrix or vector) to format.
2. output_type (optional): The type of formatting to apply to the elements. Options are 'float', 'int', or 'str'. Default is 'float'.

Example:

import numpy as np
from qudit_cirq.utils import format_out

# Define a matrix with complex elements
matrix = np.array([[1+0j, 0+0j], [0+0j, -1+0j]])

# Format the matrix as integers
formatted_matrix = format_out(matrix, output_type='int')
print(formatted_matrix)

Output:

[['1' '0']
 ['0' '-1']]

Printing the State Vector (printVector)

The printVector function prints the final state vector of a quantum circuit.

Function definition:

def printVector(final_state, dimensions, qudits=None, threshold=1e-6):
    # Function implementation

Parameters

1. final_state: The state vector (e.g., result.final_state_vector).
2. dimensions: An integer or list of integers representing the dimensions of the qudits.
3. qudits (optional): A list of qudit objects to label the qudits in the output.
4. threshold (optional): A float specifying the minimum amplitude magnitude to display. Default is 1e-6.

Example:

d = 3
qudit1 = cirq.NamedQid('q0', dimension=d)
qudit2 = cirq.NamedQid('q1', dimension=d)

circuit = cirq.Circuit()
circuit.append(quditHGate(d).on(qudit1))
circuit.append(quditHGate(d).on(qudit2))

simulator = cirq.Simulator()
result = simulator.simulate(circuit)

final_state = result.final_state_vector

# List of qudits in order
qudit_order = [qudit1, qudit2]

# Print the state vector using printVector
printVector(final_state, dimensions=[d, d], qudits=qudit_order)

Output:

Final state vector:
|00⟩: (0.3333333432674408+0j)
|01⟩: (0.3333333432674408+0j)
|02⟩: (0.3333333432674408+0j)
|10⟩: (0.3333333432674408+0j)
|11⟩: (0.3333333432674408+0j)
|12⟩: (0.3333333432674408+0j)
|20⟩: (0.3333333432674408+0j)
|21⟩: (0.3333333432674408+0j)
|22⟩: (0.3333333432674408+0j)

Tensor Product of Matrices (tensor_product)

The tensor_product function computes the tensor product of multiple matrices or vectors.

Function definition:

def tensor_product(*arrays):
    # Function implementation

Parameters

1. *arrays: A variable number of NumPy arrays to compute the tensor product of.

Example:

import numpy as np
from qudit_cirq.utils import tensor_product

# Define single-qudit states
state0 = np.array([1, 0, 0])  # |0⟩ in dimension 3
state1 = np.array([0, 1, 0])  # |1⟩ in dimension 3

# Compute the tensor product to create a two-qudit state
combined_state = tensor_product(state0, state1)

print(combined_state)

Output:

[0 1 0 0 0 0 0 0 0]

Computational Constraints

In order to assess the dimension \(d\) and the number of qudits \(n\) that can be processed in reasonable time via our library, we ran a simple test on a computer with the specification: AMD Ryzen 5 5500U at 2.10 GHz, Radeon Graphics, 8GB RAM. We set a maximum time limit of approximately one minute per simulation run, ensuring that no single circuit execution exceeded this threshold. The circuits were built randomly using the following schema:

• Initialise a specified number \(n\) of qudits at dimension \(d\).
• Randomly choose 10 single-qudit or two-qudit gates from \(X\), \(Z\), \(H\), and \(CX\). Thus the circuit depth is 10.
• Append measurement operations.

The results are shown in the figure below. The reported results are based on single-run scenarios for each dimension and qudit count. Additional runs and averaging could provide more robust metrics.

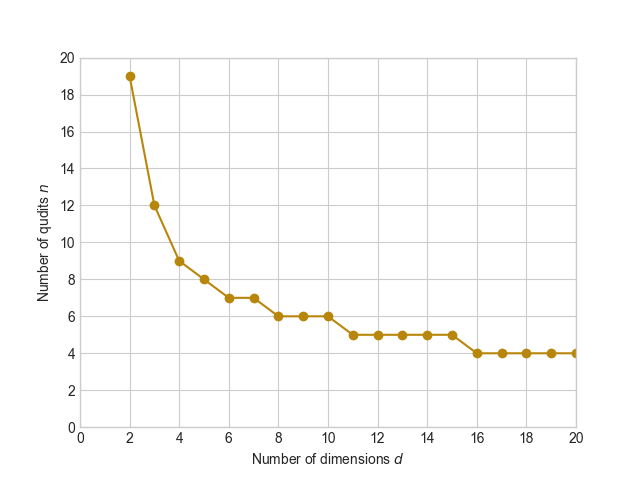
Figure: Dimension \(d\) vs Number of Qudits \(n\)

Not surprisingly, increasing the dimension results in fewer number of qudits processed within the one minute time limit imposed by us. However, by leveraging GPUs and/or quantum cloud computing services, the library should be able to handle even larger qudit circuits with greater complexity.